

Solution du cube Rubik parue dans le numéro 753 de la revue Science et vie, juin 1980
Cette méthode de résolution est utilisée par le champion du monde 2005, jean PONS.

A première vue, c'est tout bête : un cube de 56 mm de côté, formé de 27 petits cubes colorés. A chacune des faces, on peut faire subir une rotation, et mélanger ainsi en quelques secondes et inextricablement toutes les couleurs. Inoffensif ? Méfiez-vous... Quand vous l'aurez pris, vous ne pourrez plus le lâcher. Et ses 43 milliards de milliards de combinaisons ont de quoi vous faire perdre... la boule !
Fini, le « Master Mind » ! Oubliés, les « Solitaire », « Taquin » et autres « Baguenaudier » ! Au vestiaire, les gadgets électroniques joueurs d'échecs et de bataille navale ! Comparés au niveau venu, le « Rubik's Cube » ( Pour mieux suivre cet article, les lecteurs qui le désirent peuvent se procurer le cube, dans un magasin spécialisé ou dans les grandes surfaces, où il est également commercialisé. Le prix devrait varier entre 60 et 65 F.), la plupart des casse-tête ressemblent à des distractions pour attardés mentaux...
L'objet n'a l'air de rien : un cube de plastique tout simple ; 6 faces, 9 carrés de couleur sur chaque face ; tous les carrés peuvent changer de position, à l'exception de ceux qui occupent le centre de chaque face. Au départ, chaque face est unicolore. Mais attention ! Il suffit de quelques rotations effectuées au hasard sur les faces pour transformer ce bel ordre en un inextricable fouillis de couleurs. Le but du jeu étant, bien sûr, de rétablir l'ordre initial.
Voilà pour l'invention. L'inventeur ? Ernö Rubik, hongrois, sculpteur et architecte, professeur à l'Ecole des Arts décoratifs de Budapest. Signes particuliers : grand amateur d'échecs, n'est pas particulièrement doué pour les mathématiques... Ajoutons : futur millionaire, depuis qu'un entreprenant homme d'affaires français, Bernard Farkas, s'est avisé que le petit cube pouvait produire un grand choc. Il a réussi à en convaincre le groupe Ideal-Toy -- l'une des cinq premières sociétés mondiales de jeux et jouets, créateur notamment du fameux ourson « Teddy Bear ». Résultat : une commande de 6 millions de Rubik's Cubes qui seront fabriqués par les Hongrois à destination de l'exportation. Le plus gros contrat jamais signé par la Hongrie en ce domaine !
Mais qu'a-t-il donc de spécial, ce cube ? D'abord son mécanisme, aussi
simple qu'ingénieux (voir encadré pp. 138-139). Chaque face peut
tourner sur elle-même, autour d'un axe passant par son centre. De sorte
que le carré central d'une face occupe toujours la même position par
rapport aux autres faces (même s'il pivote sur lui-même). En revanche,
les quatre petits cubes qui forment les coins d'une face, tout comme les
quatre qui forment ses bords, sont déplacés à chaque rotation de la
face.
NI AIMANT, NI RESSORT: TOUT PIVOTE!
1. Le mécanisme du Rubik's Cube est d'une ingéniosité
diabolique... Chaque face peut tourner autour de sa
facette centrale, dans le sens des aiguilles d'une montre
ou dans le sens inverse.
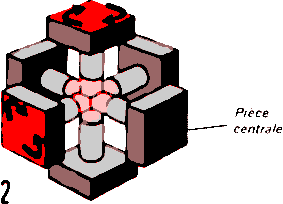
2. Les six pièces centrales sont fixées aux axes d'une
croix à six branches. Elles peuvent tourner sur elles-mêmes mais gardent toujours la même disposition les
unes par rapport aux autres.
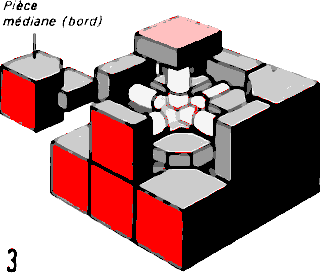
3. Les autres pièces s'emboîtent grâce à des tenons, pour former les six
faces du cube. Les douze pièces médianes (bords) ont chacune deux
facettes colorées qui apparaissent sur deux faces adjacentes.
4. Les huit pièces d'angle (coins) ont chacune trois facettes colorées qui
apparaissent sur trois faces formant trièdre.


Toutes les transformations que l'on peut faire subir aux Rubik's Cube sont basées sur le même mouvement élémentaire : une rotation de 90°, soit un quart de tour, dans le sens des aiguilles d'une montre ou dans le sens contraire, imprimée à l'une quelconque des six faces. Comme chacun de ces mouvements élémentaires modifie la configuration du cube, et que l'on peut réaliser des séries de tels mouvements aussi longues que l'on veut, le nombre de configurations possibles est immense.
Combien exactement ? Pour le savoir, il faut introduire quelques notions mathématiques. Tout d'abord, appelons permutation toute manipulation que l'on peut effectuer sur le cube, c'est-à-dire toute suite finie de rotations élémentaires. D'une manière générale, une permutation est une opération qui modifie l'ordre d'un ensemble fini d'objets : écrire les lettres de l'alphabet à 'l'envers (z, y, x, w...), battre un jeu de cartes, par exemple. Les permutations sur un ensemble donné forment ce que l'on appelle un groupe. En mathématiques, les groupes de permutations jouent un rôle essentiel pour certains problèmes : c'est, par exemple, en s'appuyant sur leurs propriétés qu'Evariste Galois a pu démontrer, au siècle dernier, que l'équation du cinquième degré n'était pas soluble par radicaux.
Remarquons maintenant que calculer le nombre de configurations possibles du Rubik's Cube revient à calculer le nombre de permutations. Précision : si deux suites distinctes de rotations élémentaires produisent le même effet, elles définissent la même permutation ; il est évident qu'il y a une infinité de telles suites, mais il est tout aussi évident que le cube ne peut prendre qu'un nombre fini de configurations (puisqu'il y a un nombre fini de faces, un nombre fini de petits carrés sur chaque face, un nombre fini de couleurs pour chaque petit carré).
Considérons le cube dans sa position de départ. Pour chacune de ses configurations possibles, il existe une permutation qui fait passer le cube de sa position initiale à cette configuration. Inversement, chaque permutation est parfaitement définie par l'effet qu'elle produit sur la position de départ. Il y a donc exactement autant de permutations que de configurations accessibles à partir de la position de départ (la « permutation identique », en abrégé I, est celle qui laisse le cube inchangé).
Pour calculer le nombre de permutations du Rubik's Cube, il faut regarder d'un peu plus près ce qui se passe lorsqu'on fait tourner les faces colorées. La première idée qui vient à l'esprit est qu'exception faite des facettes centrales (entondons par facette chacun des petits carrés qui constituent une face), toutes les facettes se meuvent indépendamment les unes des autres et peuvent donc prendre n'importe quelle couleur. La réalité est un peu plus subtile.
Considérons, pour commencer, une rotation élémentaire appliquée à la face supérieure du cube, disons un quart de tour dans le sens des aiguilles d'une montre. Qu'advient-il des coins ? Appelons A l'un quelconque des coins de la face supérieure, B, C et D les autres (toujours dans le sens des aiguilles d'une montre). La rotation d'un quart de tour déplace le petit cube, qui occupait la position A en B, le coin B en C, C en D, D en A. Mais, chose importante, les coins restent des coins. Pour les bords, on a un mouvement analogue : si ces bords sont notés A', B', C', D', ils deviennent B', C', D', A'. Si l'on avait opéré la rotation inverse (sens contraire aux aiguilles d'une montre), les coins A, B, C, D seraient devenus D, C, B, A, avec le mouvement analogue pour les bords. Morale de l'histoire : les coins restent des coins et les bords des bords.
Cela reste valable, non seulement pour une rotation élémentaire, mais pour n'importe quelle permutation du Rubik's Cube. La raison en est que toutes les permutations sont des suites de rotations élémentaires. D'ailleurs, il suffit de manipuler le cube quelque temps pour se convaincre de la chose. Impossible, donc, d'amener l'une des huit pièces qui forment les coins dans la position de l'un des douze bords, ou inversement.
Nous pouvons déduire de la manipulation élémentaire ci-dessus un autre résultat : c'est que la permutation totale qu'elle opère sur les coins et les bords est paire. Qu'est-ce que cela signifie ? Qu'elle se décompose en un nombre pair de transpositions. Qu'est-ce qu'une transposition ? C'est une permutation qui échange deux éléments sans toucher aux autres. Par exemple, la transposition (A, B) transforme les quatre coins A, B, C, D en B, A, C, D. Toute permutation peut être décomposée sous la forme d'une série de transpositions. La rotation considérée plus haut, qui transforme les coins A, B, C, D en B, C, D, A peut être obtenue en appliquant successivement les trois transpositions (A, B), (A, C), (A, D). De la même façon, l'application successive des trois 'transpositions (A', B'), (A', C'), (A', D') transforme A', B', C', D' en B', C', D', A'. Au total, la permutation qui consiste à faire tourner une face du cube d'un quart de tour se décompose donc en six transpositions, dont trois portent sur les coins et trois sur les bords. C'est une permutation paire. Le raisonnement a été explicité ici pour la rotation dans le sens des aiguilles d'une montre, mais il est exactement le même dans l'autre sens.
Comme toutes les permutations du Rubik's Cube sont des suites de rotations élémentaires (on dit aussi des produits), il en résulte qu'elles sont toutes paires : le produit de deux permutations paires est pair, tout simplement parce que la somme de deux nombres pairs est encore un nombre pair.
Nous pouvons calculer maintenant le nombre de configurations du Rubik's Cube. Les huit coins peuvent être permutés ensemble de n'importe quelle manière, ce qui donne 8! possibilités (8! - qui se prononce « factorielle huit » - est égal à 8x7x6x5x4x3x2x1) ; en effet, le premier coin peut occuper n'importe laquelle des huit positions, soit huit choix possibles ; lorsque ce choix est fait, il reste sept possibilités pour un second coin ; ce qui donne 8x7 possibilités ; pour le troisième coin, il n'y a plus que six possibilités, et ainsi de suite.
En raisonnant de la même manière sur les douze bords, on arrive à la conclusion qu'à chacune des 8! dispositions des coins, correspondent 12! choix possibles pour les bords, ce qui conduit à 8! X 12! dispositions possibles pour l'ensemble des pièces, coins et bords. En fait, il faut diviser ce nombre par deux, car les permutations doivent être paires, comme il a été vu plus haut. Or, dans n'importe quel groupe de permutation, il y a autant de permutations paires que d'impaires.
Jusqu'ici, nous n'avons considéré que la dispositon des pièces, sans tenir compte de leur orientation. Or chaque coin possède trois orientations, puisqu'il a trois facettes colorées. Les bords possèdent, eux, deux orientations. Par des manipulations appropriées, il est possible de faire « basculer » les bords ou de faire « tourner » les coins, de sorte que l'on peut orienter à volonté coins et bords. A une restriction près : lorsque l'on a choisi l'orientation de 7 coins, celle du huitième est imposée ; de même, une fois fixée l'orientation de onze bords, celle du douzième est déterminée (cela résulte de la construction du cube).
Si l'on tient compte des orientations, il y a (8!x12!)/2 x (38/3) x (212/2) donc configurations possible du Rubik's
Cube, soit très exactement :
43 252 003 274 489 856 000 possibilités !
Le numérateur représente le nombre total de manières dont on peut assembler le cube (en le démontant éventuellement). Le dénominateur 12 exprime qu'il y a 12 orbites distinctes de configurations (une orbite est l'ensemble des configurations accessibles, à partir d'une situation initiale donnée, par application de notre groupe de permutations). Il est impossible de passer d'une orbite à une autre par simple permutation, sans démonter le cube.
Un ordinateur qui énumèrerait les configurations à raison d'une par microseconde mettrait la bagatelle de 1,4 million d'années à les compter toutes... Cela n'empêche pas Emö Rubik de reconstituer son cube en 2 minutes 10 secondes, et sans l'aide d'aucune machine.
Prévenons toutefois les masochistes qui seraient tentés de se lancer sans plus de précaution dans l'aventure : si le cube est vraiment en désordre, deux semaines semblent être le temps moyen nécessaire pour trouver la solution, à condition de travailler dur et d'être plutôt doué (estimation due à David Singmaster, professeur de mathématiques à l'institut « Polytechnic of the South Bank », à Londres, dont les travaux ont inspiré cet article).
Note de Sylvain : et qui n'a fait appel a aucun "calcul de la théorie des groupes" pour trouver le premier une méthode systématique de résolution du Cube. J'étais à Londres l'été où a paru son livre et je l'avais parcouru, sans l'acheter. Il y avait la description de la méthode avec des schémas du cube très clairs, en noir et blanc, mais pas la moindre trace de "théorie des groupes".
Il est donc recommandable de s'entraîner d'abord sur des manipulations
simples. Commencez par reconstituer une face à une seule couleur.
Avec un peu d'entraînement, vous en obtiendrez deux, puis trois ou
quatre. Il n'est pas plus difficile de reconstituer les six faces que d'en
reconstituer trois ou quatre.
Attention :les facettes centrales ne pouvant pas bouger les unes par rapport aux
autres, pour réaliser une face, il faut installer les huit autres facettes de
la même couleur autour de l'élément central.
Un point important : toutes les permutations peuvent être inversées.
Même après 150 mouvements, il est possible de revenir à la situation
initiale : il suffit de reproduire exactement les mêmes mouvements, mais
dans l'ordre inverse et en sens inverse (précaution utile : notez les
mouvements au fur et à mesure, en vous servant de la notation de
l'encadré p. 136).
Un algorithme, encadré à gauche, vous permet, avec un peu
d'expérience, de reconstituer le cube en un maximum de 277 rotations
de faces (un quart de tour ou un demi-tour). Cet algorithme, dû à David
Singmaster tout comme les deux processus de base sur lesquels il
repose (voir encadré p. 136), n'est certainement pas le meilleur.
Son auteur en a d'ailleurs trouvé une version améliorée. Nous l'avons retranscrit à titre d'exemple, après avoir constaté qu'il marche effectivement.
Pour décrire toutes les manipulations que l'on peut faire sur le Rubik's Cube, une notation est nécessaire. En voici une:
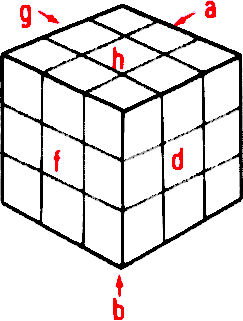
les six faces du cube sont désignées par les lettres h (haut), b (bas), g (gauche), d (droite), (face), a (arrière), comme sur la figure ci-contre.
Cette notation est indépendante des couleurs et ne se réfère qu'aux positions. Chaque bord peut alors être représenté par les deux lettres des faces auxquelles il appartient : hf désigne la pièce située en haut et face à l'observateur, db celle en bas à droite, et ainsi de suite. De même, pour les coins, on utilise les trois lettres des trois faces dont ils font partie : on a ainsi les coins fgh, fhd, dha, ahg, fbd, bfd. dba, bag. Enfin, les rotations élémentaires des faces sont désignées par des lettres capitales : F signifie une rotation d'un quart de tour et dans le sens des aiguilles d'une montre de la face f, G la même rotation pour la face G. etc. Pour indiquer des suites de rotations, on utilise une notation multiplicative : FGH signifie, par exemple, que l'on effectue d'abord F. puis G, puis H (attention : FGH ne produit pas le même effet que FHG ou que GHF). F2 signifie que l'on fait deux fois F, et F-1 désigne la même rotation élémentaire que F, mais dans le sens inverse des aiguilles d'une montre. Avec un peu de pratique, cette notation vous paraîtra fort simple.
Nous pouvons maintenant étudier deux manipulations de base.
1
2
3
4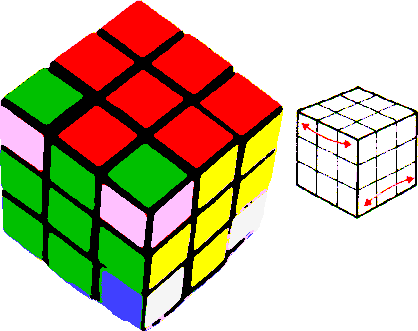
Cette séquence est basée sur le processus « COIN » = FDF-1D-1. Une première application de COIN conduit de 1 à la figure 2. une seconde à la figure 3, une troisième à 4. Trois applications supplémentaires nous ramèneraient au départ, c'est-à-dire que COIN6 = I. COIN3 qui consiste à faire trois fois COIN permet d'échanger fgh et fhd d'une part, dba et fbd d'autre part, avec des changements d'orientation, sans toucher aux bords (I est l'opération qui ne change rien).
5
6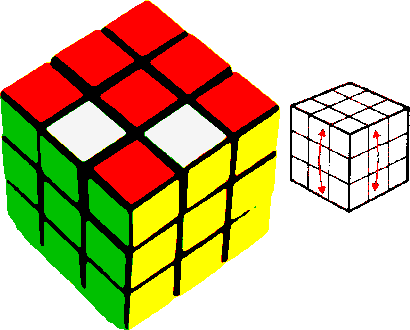
7
Ce processus, que nous appellerons « BORD », s'obtient en faisant deux fois F, puis deux fois D, et en répétant la chose trois fois, ce qui se note (F2D2)3. L'effet de BORD illustré par la figure 6, est la double transposition (fh, fb) (dh, db). Remarquons qu'en effectuant BORD une deuxième fois, on retrouve la situation initiale 7, ce qui s'écrit BORD2 = I, autrement dit BORD est son propre inverse.
N.B. - Les processus COIN et BORD sont ici appliqués aux faces f et d, mais on peut évidemment choisir n'importe quel couple de faces adjacentes : par exemple BORD (d, h) = (D2H2)3, etc.
En combinant les deux processus COIN et BORD, il est possible de
reconstituer les six faces du Rubik's Cube. Voici la démarche générale
:
1. Mettre en place les quatre coins du bas, c'est-à-dire dans la bonne
position et avec la bonne orientation (pas de méthode particulière).
2. Si les coins du haut sont dans une permutation impaire, faire H.
3. Faire plusieurs COIN pour placer les quatre coins du haut dans la
bonne position.
4. Faire plusieurs COIN2 pour tourner les coins vers le haut dans la
bonne orientation.
5. Faire plusieurs BORD pour mettre tous les bords dans la bonne
position avec la bonne orientation.
Attention : l'exécution des étapes 3, 4 et 5 nécessite le recours à une
astuce supplémentaire, la « conjugaison ». L'idée est la suivante : si l'on
veut par exemple effectuer la double transposition (hf, ha) (hd, hg) à
l'aide de BORD, il faut d'abord faire FA-1H pour obtenir la situation où
BORD s'applique. On fait alors BORD appliqué aux faces d et h, soit
BORD (d, h) = (D2H2)3 puis H-1AF-1 donne la configuration désirée.
L'opération totale s'appelle un conjugué de BORD. D'une manière
générale, un conjugué fait la même opération que le processus initial,
mais sur des objets différents.
Bien entendu, nous invitons les lecteurs qui trouveraient de meilleures solutions à nous les communiquer (il en existe beaucoup). Et maintenant, à vous de jouer !
Michel de PRACONTAL